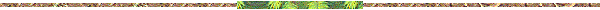retour aux autres reportages 

Albert Art. Docteur en sciences.

Comment des oiseaux aquatiques, parfois pesant plusieurs kilos, parviennent-ils à flotter ?
Un naturaliste dira, la nature a bien fait les choses, un physicien tentera d'expliquer cet équilibre à partir de concepts, tels que : la force gravitationnelle, le centre de gravité, la poussée d'Archimède, le centre de poussée, le couple de forces. Le grand mystère est de savoir à quel moment les principes qui régissent la nature et par la suite les sciences sont apparus. A cette question personne ne peut actuellement répondre.
Le texte a été conçu pour être lu en sautant les parties en italique qui apportent des explications plus scientifiques.

Elle est due à l'attraction de la Terre sur l'oiseau, elle n'est autre que son poids. Cette force gravitationnelle est appliquée (attachée) au centre de gravité C de l'oiseau. Tout se passe alors comme si cette force était seule à agir sur lui en ce point.

Essayons de comprendre d'où vient le poids total de l'oiseau. Pour la facilité, on le considérera comme étant homogène. Découpons le, par la pensée, en petits cubes. Ils n'ont pas tous été dessinés. Chacun d'eux subit l'attraction terrestre et a donc un poids comme représenté par la flèche sur le cube séparé. L'ensemble de toutes ces petites forces (la somme vectorielle) est équivalent à une seule force qui représente le poids de l'oiseau et qui est appliquée en son centre de gravité C. Quand les cubes sont très très petits ils remplissent tout le volume de l'oiseau.

On peut l'imaginer comme étant le résultat de la réduction progressive du canard, (supposé homogène) tout en gardant sa forme jusqu'à ce qu'il soit réduit à un point appelé centre de gravité. C'est en ce point qu'est appliquée la force gravitationnelle, notée Fg, qui représente son poids. Fg est toujours dirigée vers le centre de la terre, c'est-à-dire suivant la verticale du lieu.
Ci-dessous des oies au repos sur une patte, sont en équilibre sur le sol. En A, vue de profil, la verticale et la patte sont parfaitement alignées. En B, vue de dos, on voit que l'oie a incliné sa patte de façon à ce que la verticale aboutisse au milieu de la palme. Si ce n'était le cas elle tomberait. En C même situation qu'en B. Dans ces trois cas, la patte soutient tout le poids de l'animal. A la vue de ces oies en équilibre, on peut affirmer que le centre de gravité se trouve quelque part sur la verticale, mais où ? Pour le savoir il faudrait faire des expériences difficiles à réaliser avec un oiseau.

        

Les molécules d'un fluide sont continuellement en mouvement, ce qui provoque des chocs sur les surfaces de tout objet introduit dans ce fluide tel que l'eau. Ces chocs sont à l'origine de la pression.
Cette pression augmente avec la profondeur comme le prouve la douleur ressentie au niveau du tympan quand on plonge profondément sous l'eau. Lorsqu'elle agit sur une surface, elle engendre une force, appelée force de pression, qui est perpendiculaire à cette surface. Sa valeur dépendra à la fois de la superficie S de la surface en contact avec le fluide (ici, l'eau) et de la pression p.
Sur le dessin, représentant un canard sur l'eau, les flèches symbolisent les forces de pression s'exerçant perpendiculairement sur chaque petite partie de sa surface immergée. L'ensemble de ces forces donne une force totale appelée la poussée d'Archimède. C'est elle qui tend à « pousser » le canard vers le haut pour qu'il ne coule pas sous l'action de son poids.
C'est au centre de gravité du volume déplacé (occupé), comme le montre le dessin de la bouteille complètement immergée. Ce centre est appelé centre de poussée.

Une relation simple permet de calculer la valeur de cette force de pression f. Elle est égale au produit de la pression p par la superficie s de la surface sur laquelle la pression agit : f = p x s. Par conséquent, sur chaque petite surface s qui compose la surface immergée de l'oiseau s'exerce une petite force de pression f.
En réalité, c'est la somme vectorielle de toutes les composantes verticales (dessin, au dessus à gauche) de ces petites forces qui donne la poussée d'Archimède sur le canard. Elle est représentée par une seule grande force appliquée au centre de gravité (c) du volume d'eau déplacé (en jaune sur le dessin), appelé centre de poussée. Remarquons que les flèches sont perpendiculaires aux surfaces s. Leurs grandeurs indiquent que la force de pression varie avec la profondeur, c'est-à-dire avec la pression p, pour des surfaces s identiques.

Quelle est la valeur de cette poussée ? Elle est égale au poids du volume d'eau déplacé (la partie jaune sur le dessin) par l'oiseau quand il est sur l'eau.

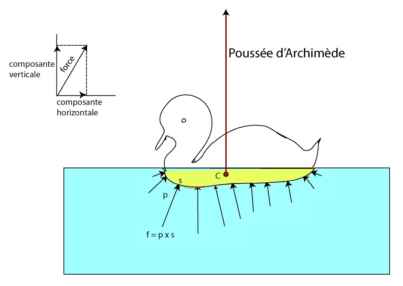
Une expérience simple permet d'en déterminer la valeur. Plongeons complètement dans l'eau une bouteille (supposée sans poids) remplie d'eau. Le volume de la bouteille pleine d'eau est coloré en bleu (Fig. D) et on a représenté (Fig. E) une bouteille imaginaire colorée en vert et en pointillés, pour symboliser le volume d'eau occupé (déplacé) par la bouteille.
On observe expérimentalement qu'elle ne coule ni ne flotte, elle reste là où elle est mise. La raison est qu'à l'équilibre, il y a égalité entre le poids de l'eau dans la bouteille (vers le bas).et la poussée (vers le haut) dont la valeur est équivalente au poids de l'eau déplacée (en vert) comme montré ci-dessous.

    

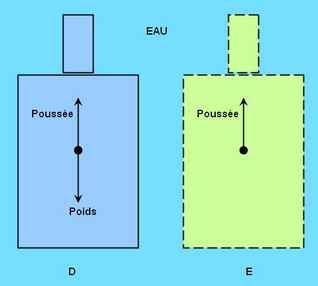
La surface de la bouteille immergée sera soumise aux forces de pression f (f₁, f₂, f_L) toutes perpendiculaires à celle-ci (dessin de droite). Sur la partie cylindrique, ces forces latérales sont horizontales (f_L) et s'annulent deux à deux. Elles n'ont donc pas d'influence sur la poussée. Sachant que la pression p dépend de la profondeur h par la relation : p = d x g x h (d = densité du fluide, g = constante gravitationnelle, h = la profondeur), on déduit que, sur la surface de base s₁ située à une profondeur h₁ s'exerce une force f₁ égale à s₁ x d x g x h₁, de même sur s₂ à la profondeur h₂, la force f₂ sera : s₂ x d x g x h₂. Ici la superficie s₁ étant égale à s₂, on posera : s₁ = s₂ = s. Ces deux forces agissant en sens opposé, la force totale sur le cylindre sera égale à leur différence : (s x d x g x h₂) - (s x d x g x h₁) = s x d x g (h₂ - h₁), d'où f totale = d x g x s x H, avec H = (h₂ -h₁) la hauteur du cylindre. Le produit de s x H est le volume de l'eau occupé (déplacé) par le cylindre qui multiplié par g et d, donne le poids du fluide (déplacé) occupé.

Conclusion :
La valeur de la poussée d'Archimède est égale à la somme (vectorielle) de toutes les forces de pression agissant sur l'objet, ici l'oiseau. Cette somme équivaut au poids du volume d'eau déplacé (occupé).

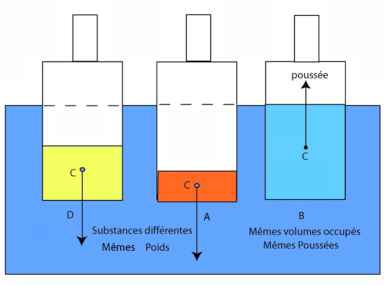
Généralisons. Si la bouteille est totalement remplie avec une substance plus « lourde » que l'eau, elle coule, si elle est remplie avec une substance plus « légère » que l'eau, elle flotte.
Maintenant si la bouteille est remplie partiellement avec des substances plus « lourde » que l'eau (en orange ou en jaune) elle flottera à condition que la poussée soit égale au poids de la substance qu'elle contient. Sa valeur équivaudra au poids du volume d'eau déplacé par la bouteille (en bleu clair) (Fig. B).
La poussée, pour des substances différentes (D et A) contenues dans la bouteille mais de mêmes poids, ne change pas de valeur, puisqu'elle ne dépend que de l'action des forces de pression de l'eau sur sa surface. La bouteille s'enfoncera donc de la même manière dans les deux cas et la poussée sera la même.

L'oiseau aquatique, qui peut être considéré comme une sorte de récipient rempli de différentes substances (air dans les plumes, os, muscles, viscères, plumes, etc.), sera en équilibre sur l'eau si la poussée est égale à son poids et équivalente au poids du volume d'eau déplacé.

Pour savoir si un corps flottera, il suffit d'en connaître sa densité moyenne D_corps, c'est-à-dire le rapport entre son poids et son volume total comparé au poids du même volume d'eau.
Si D_corps est plus grande que 1, il coule ; si elle est plus petite que 1, il flotte. La densité de l'eau étant égale à 1. Exemple : un cygne pèse des kilos, mais son volume est énorme. Le rapport entre ces deux grandeurs donne la densité moyenne du cygne. Si elle est inférieure à 1, il flottera.

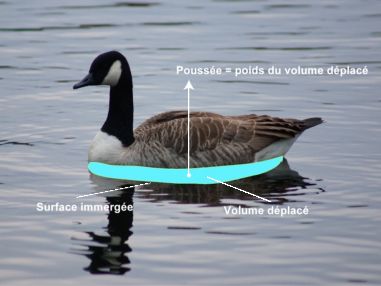
Cette oie en entrant dans l'eau a déplacé un certain volume d'eau (partie colorée) qui provoque automatiquement l'apparition de la poussée d'Archimède dont la valeur est donnée par le poids du volume déplacé.

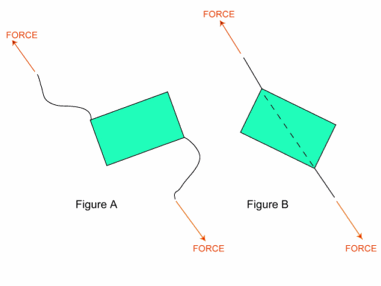
Prenons un morceau de carton et attachons deux trombones disposés face à face. Attachons une ficelle à chaque trombone, de façon non alignée comme le montre la figure A.
Tirons sur les deux ficelles en agissant avec deux forces opposées. Elles finiront par se trouver alignées comme le montre la figure B.

Quand deux forces, formant un couple, agissent sur un objet, elles font tourner l'objet jusqu'à ce qu'elles soient alignées. Si ces forces sont égales et de sens contraires, après la rotation, l'objet restera en place.

Et les oiseaux aquatiques ? S'ils sont sur l'eau sans nager, ils sont soumis, rappelons-le, à deux forces : le poids et la poussée. C'est donc ce couple de forces « poids-poussée » qui va agir sur l'oiseau de la même manière que les deux ficelles sur le carton : la poussée tire vers le haut et le poids tire vers le bas de sorte que l'oiseau prendra une situation stable dès que ces deux forces seront alignées. On peut alors imaginer une infinité de possibilités. Nous en choisirons quatre caractéristiques parmi elles.

Figure A : Situation possible théoriquement mais heureusement pour les oiseaux aquatiques elle n'est jamais observée.
Figure B : L'oiseau pourrait être « mal conçu » et être plus pesant vers l'arrière, ce qui déplacerait son centre de gravité vers l'arrière puisque le nombre de petits cubes y serait plus grand. Le couple de forces « poids-poussée » lui fera alors prendre cette position « cabrée ».
Figure C : même processus qu'en B sauf que le poids serait déplacé vers l'avant.
Figure D : C'est la situation généralement observée dans la nature. L'oiseau est « bien conçu » et dans ce cas les petits cubes sont judicieusement répartis. Dans ces conditions la poussée et le poids sont d'emblée naturellement alignés, l'oiseau se trouvera donc à l'équilibre quasi à l'horizontale.

La physiologie des oiseaux plongeurs est telle qu'ils peuvent plonger facilement et nager sous l'eau sans effort. C'est principalement la position rapprochée du centre de gravité et du centre de poussée qui en est responsable. Dans ce cas il doit fournir moins d'effort pour « basculer » et entrer sous l'eau.

Ce canard plongeur qui possède cette propriété, est en position de plongée adoptée par la majorité des plongeurs. Il commence par vider ses sacs d'air, puis à l'aide de ses pattes, il fait sortir son corps de l'eau, ce qui facilite le mouvement d'entrée dans l'eau.

Par contre d'autres, comme le cygne, le colvert... ont de grandes difficultés à plonger, les deux centres sont plus éloignés l'un de l'autre, ils se contentent alors de culbuter et de se maintenir dans cette position grâce aux mouvements de leurs pattes.

C'est grâce à l'imperméabilité de leurs plumes que la plupart des oiseaux aquatiques ne se mouillent pas lorsqu'ils sont en contact avec l'eau. Ils possèdent en effet, un système de « graissage » de leurs plumes. On compte environ 1 000 plumes et représente le tiers du poids de l'oiseau (valeurs approximatives).

Ce cygne noir vient de plonger sa tête sous l'eau. Celle-ci reste sous forme de gouttelettes et ne mouille donc pas les plumes. Sans ce système, l'eau prendrait la place de l'air contenue dans le plumage, ce qui aurait une double conséquence :
- Le poids de l'oiseau augmenterait fortement ce qui détruirait son équilibre et il risquerait de couler.
- Le contact permanent de l'eau avec son corps lui ferait perdre une grande quantité d'énergie surtout l'hiver. Sa vie en serait menacée.

Le cormoran qui pêche sous l'eau est une exception. Il a des plumes qui se mouillent partiellement après un certain temps de plongée. Ceci lui donne l'avantage d'augmenter son poids qui s'oppose en partie à le faire remonter vers la surface à cause de la poussée. Il reste donc plus facilement sous l'eau, ce qui lui permet de dépenser moins d'énergie pour pêcher. Après une plongée, pour pouvoir soit s'envoler facilement, soit pêcher à nouveau, il doit sécher ses plumes, ce qu'il fait en ouvrant ses ailes pour les exposer au vent et au soleil.